Lektion
   Brüche addieren und subtrahieren   
Hilfe
Diskutieren
Panik-Test
Themenübersicht
zu den Übungsaufgaben
Worum geht es?
Genauso wie man normale Zahlen ständig addieren und subtrahieren muss, möchte man auch mit Bruchteilen Plus und Minus rechnen.

Ein Viertel Liter Farbe aus diesem Eimer, ein Drittel aus jenem und zwei Fünftel aus einem weiteren Eimer werden zusammen geschüttet. Wie viel Farbe ergibt das insgesamt?
 

   
In dieser Lektion lernst du:
1.Addieren und Subtrahieren von Brüchen mit gleichem Nenner.
2.Addieren und Subtrahieren von Brüchen mit verschiedenem Nenner.
3.Addieren und Subtrahieren von gemischten Zahlen.
  
Addieren und Subtrahieren bei gleichem Nenner.
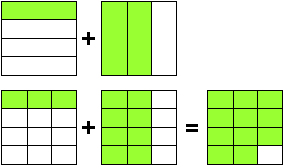
Einfach!  Super einfach!!!

Drei Achtel und vier Achtel ergibt? Na???
Sieben Achtel, klar, was denn sonst!

Haben beide Brüche den gleichen Nenner, sind also die Bruchstücke gleich groß, muss man einfach nur die Anzahl der Stücke zusammen zählen. Man muss lediglich die Zähler addieren, der Nenner bleibt wie er war.

3
8
 + 
4
8
 = 
7
8


5
12
 + 
4
12
 = 
9
12


Das Gleiche gilt natürlich, wenn man subtrahiert:

5
6
 – 
3
6
 = 
2
6


17
10
 – 
11
10
 = 
6
10
  
Merke:
gleichnamige Brüche:
Haben beide Brüche den gleichen Nenner, müssen nur die Zähler addiert oder subtrahiert werden.









      
Brüche mit gleichem Nenner heißen "gleichnamig".
Addieren und Subtrahieren bei verschiedenem Nenner.
Nicht mehr so einfach!

Brüche mit verschiedenem Nenner können nicht einfach so zusammen gezählt werden, denn die Bruchstücke sind ja nicht mehr gleich groß!

Ein Viertel und zwei Drittel? Schwierig!

1
4
 + 
2
3
 = ???
 


 





    
Merke:
ungleichnamige Brüche:
Haben die Brüche verschie­dene Nenner, bringt man sie zunächst auf den gleichen Nenner. Anschließend können die Zähler addiert oder subtrahiert werden.







     
Der Hauptnenner

ist das kgV, das kleinste gemeinsame Vielfache der beiden Nenner.

(siehe 5. Klasse)




Es gibt nur einen Weg: Beide Brüche müssen so umgeformt werden, dass sie in gleich großen Stücken gezählt werden.

Man muss sie also so erweitern, dass sie den gleichen Nenner erhalten. Danach kann man dann addieren:

1
4
 + 
2
3
 = 
3
12
 + 
8
12
 = 
11
12
  
Weitere Beispiele:

3
5
 + 
7
10
 = ???

Zuerst auf den gleichen Nenner bringen (den Hauptnenner), dann die Zähler addieren:

3
5
 + 
7
10
 = 
12
20
 + 
14
20
 = 
26
20
  
3
8
 – 
1
6
 = 
9
24
 – 
4
24
 = 
5
24
  
Am Ende einer Rechnung schaut man immer, ob das Ergebnis nicht noch gekürzt werden kann. Außerdem kontrolliert man, ob der Zähler vielleicht größer ist, als der Nenner. In diesem Fall schreibt man den Bruch als gemischte Zahl.

3
4
 + 
2
5
 = 
15
20
 + 
8
20
 = 
23
20
 = 1
3
20
  
Addieren und Subtrahieren von gemischten Zahlen
Gemischte Zahlen addiert oder subtrahiert man, indem man die natürlichen Zahlen und die restlichen Brüche getrennt verrechnet.
 


Merke:
Bei gemischten Zahlen verrechnet man die natürlichen Zahlen und die Brüche getrennt.
3
2
5
 + 2
1
4
 = 3
8
20
 + 2
5
20
 = 5
13
20


4
1
3
 + 3
2
6
 = 4
2
6
 + 3
2
6
 = 7
4
6
 = 7
2
3
  
Natürlich muss man auch hier schauen, ob man den Bruch im Ergebnis nochmal kürzen kann, oder ob im Bruch der Zähler größer ist als der Nenner.
 
5
3
4
 – 4
1
4
 = 1
2
4
 = 1
1
2


4
5
 + 1
3
10
 = 
8
10
 + 1
3
10
 = 1
11
10
 = 2
1
10


Zehn Zehntel wurden wieder zu einem Ganzen.
 
Unangenehm wird es, wenn beim Subtrahieren der erste Bruch kleiner ist als der zweite. In diesem Fall muss man sich etwas von der ganzen Zahl "borgen":
 
7
1
4
 – 1
3
4
 = 6
5
4
 – 1
3
4
 = 5
2
4
 = 5
1
2


Weil das eine Viertel zum Subtrahieren zu klein ist, haben wir uns vier Viertel von den 7 Ganzen geborgt.
 

Fehler gefunden oder Anregungen?