|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||
|
Größere Zahlen kann man nicht mehr im Kopf subtrahieren. Hier muss man schriftlich arbeiten. Aber Achtung: Gerade beim Übertrag passieren leicht Fehler.
875369
– 648105 = ??? |
 |
||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
| So subtrahiert man schriftlich: | |||||||||||||||||||||||||||||||||||
|
Es gibt zwei Methoden: Entweder du arbeitest mit Übertrag oder du borgst dir etwas. Schau dir kurz die beiden Beispiele an und nimm die Methode, die du in der Grundschule gelernt hast.
|
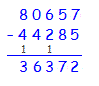
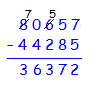
|
||||||||||||||||||||||||||||||||||
|
Methode 1 (Übetrag):
Es geht von rechts los: 7 minus 5 gibt 2. Hinschreiben! 5 minus 8 geht nicht. Also: 15 minus 8. Ergibt 7. Hinschreiben. Nun markierst du dir, dass du 15 statt 5 genommen hast. Schreibe die 1 unten zu den nächsten Zahlen dazu. Weiter: 6 minus 3 ergibt 3. Hinschreiben. 0 minus 4 geht nicht. Also: 10 minus 4. Ergibt 6. Hinschreiben. Wieder die Übertrags-Eins unten notieren. 8 minus 5 ergibt 3. Hinschreiben. Fertig. |
|||||||||||||||||||||||||||||||||||
|
Methode 2 (Borgen):
Es geht von rechts los: 7 minus 5 gibt 2. Hinschreiben! 5 minus 8 geht nicht. Also: 15 minus 8. Ergibt 7. Hinschreiben. Nun markierst du dir, dass du 15 statt 5 genommen hast. Die 1 hast du dir von der 6 geborgt. Die wird deshalb zur 5. Weiter: 5 minus 2 ergibt 3. Hinschreiben. 0 minus 4 geht nicht. Also: 10 minus 4. Ergibt 6. Hinschreiben. Wieder markieren, dass man 10 statt 0 genommen hat und sich etwas borgen musste. Dadurch wird die 8 zur 7. 7 minus 4 ergibt 3. Hinschreiben. Fertig. |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
| Mehrer Zahlen subtrahieren | |||||||||||||||||||||||||||||||||||
|
Hier muss man zunächst alle Zahlen, die subtrahiert werden sollen, zusammen zählen. Addieren! Das Ergebnis wird dann von der oberen Zahl abgezogen.
|
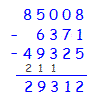  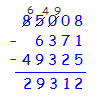
|
||||||||||||||||||||||||||||||||||
|
Methode 1 (Übetrag):
1 + 5 = 6. 8 minus 6 gibt 2. 7 + 2 = 9. 0 minus 9 geht nicht. Also: 10 – 9. Ergibt 1. Dass man 10 statt 0 genommen hat als Übertrag notieren. 3 + 3 + 1 = 7. 0 minus 7 geht nicht. 10 minus 7 gibt 3. Übertrag 1. 6 + 9 + 1 = 16. 5 minus 16 geht nicht. 15 minus 16 auch nicht. Also: 25 – 16 = 9. Übertrag 2. 8 – 6 = 2. |
|||||||||||||||||||||||||||||||||||
|
Methode 2 (Borgen):
1 + 5 = 6. 8 minus 6 gibt 2. 7 + 2 = 9. 0 minus 9 geht nicht. Also: 10 – 9. Ergibt 1. Dass man 10 statt 0 genommen hat notieren: Eins von der 0 borgen. Die 0 wird zur 9. Achtung: Die 0 kann nicht zur 9 werden. Dazu muss diese 0 zuerst eine 10 werden. Und dazu wird Eins von der 5 geborgt. Die 5 wird zur 4. 3 + 3 = 6. 9 minus 6 gibt 3. 6 + 9 = 15. 4 minus 15 geht nicht. 14 minus 15 auch nicht. Also: 24 – 15 = 9. Dazu musste man aber 2 von der 8 borgen. 6 – 4 = 2. |
|||||||||||||||||||||||||||||||||||







