|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||||||||||||
|
Um das große Feld der Architekten, Ingenieure, Konstrukteure und Künstler: Die Geometrie.
In dieser Lektion klären wir ein paar Grundbegriffe, die du in den anschließenden Lektionen und auch in den folgenden Jahren brauchen wirst. Extrem schwierig!!! ;O) |
 |
||||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Mengen, Schnitt- und Vereinigungsmengen. | |||||||||||||||||||||||||||||||||||||||||||||||
|
Mengen:
In der Mathematik haben wir es dauernd mit Mengen zu tun, also einfach einer Anzahl von Dingen. Zum Beispiel mit Zahlenmengen, wie etwa die Menge aller geraden Zahlen. Oder mit Punktmengen, wie etwa allen Punkten eines Kreises. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Mengen werden mit Großbuchstaben bezeichnet: A, B, C
Gehört ein Punkt P zur Menge A schreibt man: P ϵ A. Gehört er nicht zur Menge A, schreibt man: P ϶ A. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
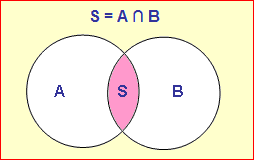
Schnittmenge:
Nun betrachten wir ZWEI Mengen. Zum Beispiel die beiden Kreisinhalte rechts. Die Menge der Punkte, die zur Menge A und zugleich zur Menge B gehören (also zu beiden Kreisen), nennt man Schnittmenge S. Man schreibt: S = A ∩ B Man liest: S ist A geschnitten B. Oder: S ist die Schnittmenge von A und B. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
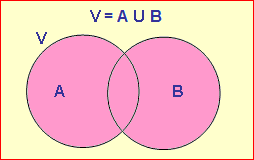
Vereinigungsmenge:
Die Menge der Punkte, die zu A oder auch zu B gehören (Sie dürfen auch gerne zu beiden gehören), nennt man die Vereinigungsmenge V. Man schreibt: S = A U B Man liest: V ist A vereinigt B. Oder: V ist die Vereinigungsmenge von A und B. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Geraden, Halbgeraden und Strecken | |||||||||||||||||||||||||||||||||||||||||||||||
|
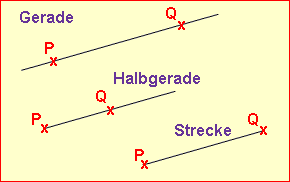
Geraden:
Mit Geraden meint man in der Mathematik eine gerade Linie, die links und rechts nicht aufhört. Als Namen gibt man ihnen Kleinbuchstaben: g, h, ... Oder man bezeichnet sie mit zwei Punkten, durch die sie hindurch laufen: PQ , DE , ... |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Halbgeraden:
Halbgeraden sind gerade Linien, die zwar bei einem Punkt beginnen. Auf der anderen Seite hören sie aber nie auf. Eine halbe Gerade eben. Man schreibt [PQ, wenn eine Halbgerade bei P beginnt, oder PQ], wenn sie bei Q endet. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Strecken:
Strecken sind gerade Linien, die bei einem Punkt beginnen und an einem anderen enden. Man schreibt [PQ], wenn eine Strecke bei P beginnt und bei Q endet. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Parallele und rechtwinklige Geraden | |||||||||||||||||||||||||||||||||||||||||||||||
|
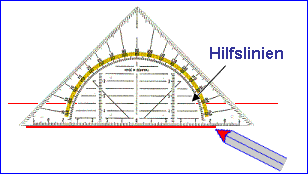
Geraden, die immer den gleichen Abstand zueinander haben, heißen parallel. Sie schneiden sich nie.
Du zeichnest sie mit Hilfe der dünnen Hilfslinien auf deinem Geodreieck. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Liegt eine Gerade NICHT parallel zu einer anderen, dann schneidet sie sie irgendwann. Dabei kann es nur einen einzigen Schnittpunkt geben.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
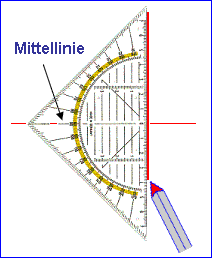
Etwas Besonderes ist es, wenn eine Gerade senkrecht zu einer anderen liegt. Solche Geraden zeichnest du mit Hilfe der Mittellinie deines Geodreiecks.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Abstände messen | |||||||||||||||||||||||||||||||||||||||||||||||
|
Den Abstand zwischen zwei Punkten misst du natürlich einfach mit einem Lineal. Das kann jeder.
|

|
||||||||||||||||||||||||||||||||||||||||||||||
|
Wie aber misst man den Abstand, den ein Punkt zu einer Geraden hat? Je nachdem, bis an welche Stelle der Geraden du misst, bekommst du eine andere Entfernung.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
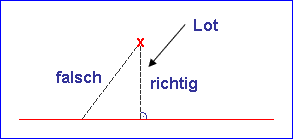
Sinnvoll ist nur eine dieser Zahlen, und zwar diejenige, die du bekommst, wenn du senkrecht zur Geraden misst. Es ist die kleinst mögliche Entfernung, die du messen kannst.
Man sagt auch: Du musst vom Punkt aus das Lot auf die Gerade fällen. (Das heißt: eine senkrechte Linie zur Geraden ziehen.) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Auf die gleiche Art misst man den Abstand zwischen zwei Geraden: Eine Senkrechte zwischen den beiden Geraden ziehen und messen.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Gerade und Kreis | |||||||||||||||||||||||||||||||||||||||||||||||
|
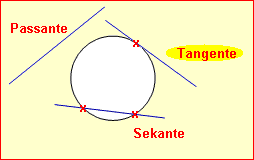
Eine Gerade kann auf drei Arten zu einem Kreis liegen:
|
 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||












