|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||
|
Hier sollst dein Wissen über Sinus, Cosinus, Tangens, den Sinussatz und den Kosinussatz anwenden, um unbekannte Streckenlängen und Winkel zu berechnen.
Häufig lässt sich die gewünschte Größe nicht direkt berechnen. Stattdessen muss man den Umweg über zwei, drei andere Größen nehmen. Die Lösungen, die du hier und in den Übungen siehst, sind nur eine Möglichkeit. In der Regel gibt es viele Wege, die zum Ziel führen. |
 |
||||||||||||

|
|||||||||||||
|
|
|||||||||||||
| Beispiel 1 | |||||||||||||
|
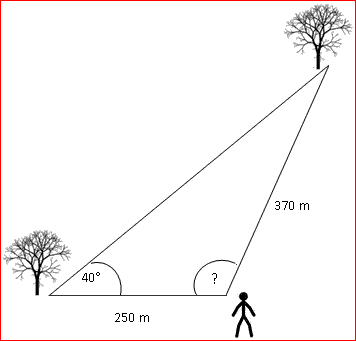
Unter welchem Winkel sieht der Beobachter die Bäume und wie weit stehen sie auseinander?
Lösung: Wir haben keine andere Wahl, als zunächst mittels Sinussatz den Winkel am entfernten Baum zu berechnen. Nennen wir ihn α.
α = 25,74° ˅ α = 154,26° |
|
||||||||||||
|
Anhand der Skizze sieht man eindeutig, dass der Winkel spitz ist. Außerdem liegt er der kleineren Seite gegenüber.
Also: α = 25,74° Damit ist der Winkel beim Betrachter: γ = 180° – 40° – 25,74° = 114,26°. Der Abstand a der Bäume: a2 = 2502 + 3702 – 2·250·370·cos 114,26° | √ a = 524,80 m |
|||||||||||||
|
|||||||||||||
| Beispiel 2 | |||||||||||||
|
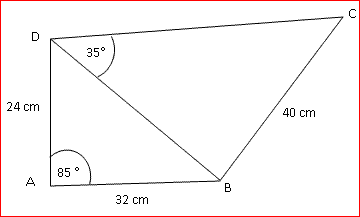
Berechne die Strecke CD.
Lösung: Mittels Kosinussatz bekommen wir BD .BD 2 = 242 + 322 – 2·24·32·cos 85° | √ BD = 38,29 cmMittels Sinussatz den Winkel bei C:
γ = 33,30° |
|
||||||||||||
|
Nun den Winkel NCBD bei B:
∡CBD = 180° – 35° – 33,30° = 111,70° Und schließlich mit dem Kosinussatz die gewünschte Strecke: CD 2 = 402 + 38,292 – 2·40·38,29·cos 111,70° | √ CD = 64,80 cm
|
|||||||||||||