|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||
|
Es gibt zwei Situationen im allgemeinen Dreieck, die man nicht mit Hilfe des Sinussatzes lösen kann: → Wenn drei Seiten gegeben sind. → Wenn zwei Seiten und der eingeschlossene Winkel gegeben sind. Wenn du in diesen Situationen den Sinussatz anwendest, bleiben in deinen Gleichungen immer zwei Variablen stehen. Keine Chance da etwas auszurechnen! Stattdessen verwendet man den Kosinussatz. |
 |
||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Der Kosinussatz | |||||||||||||||||||||||||||||
|
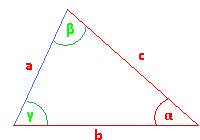
In jedem Dreieck gilt folgende Gleichung:
a2 = b2 + c2 – 2·b·c·cos α Damit kannst du a berechnen. Merke dir, wie die Gleichung aufgebaut ist. Es gibt noch zwei weitere für b und für c, die genauso aussehen. Der Kosinussatz ist eine Art Pythagoras, bei dem zum Schluss etwas korrigiert wird, weil es sich nicht um einen rechten Winkel handelt. |

|
||||||||||||||||||||||||||||
|
In Worten:
Seite zum Quadrat = zweite Seite zum Quadrat plus dritte Seite zum Quadrat minus Seite mal Seite mal Kosinus des eingeschlossenen Winkels. |
|||||||||||||||||||||||||||||
|
Alle drei Gleichungen lauten:
a2 = b2 + c2 – 2·b·c·cos α b2 = a2 + c2 – 2·a·c·cos β c2 = a2 + b2 – 2·a·b·cos γ |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Seiten berechnen | |||||||||||||||||||||||||||||
|
Am einfachsten ist es auch hier, mit Hilfe des Kosinussatzes Seiten zu berechnen.
→ Stelle den Kosinussatz für die gewünschte Seite auf. → Rechte Seite ausrechnen. → Wurzel ziehen. |
|
||||||||||||||||||||||||||||
|
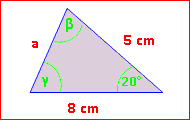
Beispiel:
Berechne im nebenstehenden Dreieck die fehlende Seite. Versuche doch zunächst einmal, den Sinussatz anzusetzen. Erkennst du, dass es nichts bringt? Also den Kosinussatz: a2 = 82 + 52 – 2·8·5·cos 20° a2 = 13,82 | √ a = 3,72 cm Nicht schwer, oder? |
|||||||||||||||||||||||||||||
|
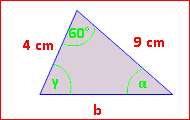
Beispiel 2:
Berechne wieder die fehlende Seite. b2 = 42 + 92 – 2·4·9·cos 60° b2 = 61 | √ b = 7,81 cm |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Winkel berechnen | |||||||||||||||||||||||||||||
|
Die Winkel zu berechnen ist etwas schwieriger, weil kräftig umgeformt werden muss.
Aber es gibt keine Alternative, wenn im Dreieck drei Seiten gegeben sind. Der erste Winkel muss dann mit dem Kosinussatz berechnet werden. Bei dem zweiten Winkel hast du anschließend die Wahl zwischen Sinus- und Kosinussatz. Bedingung: Drei Seiten sind gegeben. → Stelle den Kosinussatz für die Seite auf, die dem Winkel gegenüber liegt. → Löse ihn nach dem Winkel auf. → Ausrechnen, [SHIFT] [cos] und fertig. Das gute dabei: Der berechnete Winkel ist eindeutig! |
Beim Kosinussatz
ist der berechnete Winkel eindeutig! 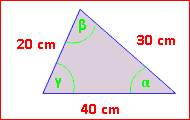
Den zweiten Winkel kann man auch mit dem Sinussatz berechnen. Allerdings ist er dann nicht eindeutig.
|
||||||||||||||||||||||||||||
|
Beispiel:
Berechne im nebenstehenden Dreieck die fehlende Winkel. Zuerst α. Der Kosinussatz, in dem α vorkommt, ist der für a: a2 = b2 + c2 – 2·b·c·cos α 202 = 402 + 302 – 2·40·30·cos α 400 = 2500 – 2400·cos α | – 2500 :(-2400)
cos α = 0,875 α = 28,96° |
|||||||||||||||||||||||||||||
|
Eine etwas wilde Rechnerei oder Tipperei, aber du wirst dich dran gewöhnen! Viele Schüler lassen die Zwischenschritte weg und tippen alles gleich richtig umgeformt in den Taschenrechner ein.
Nun β: b2 = a2 + c2 – 2·a·c·cos β 402 = 202 + 302 – 2·20·30·cos β cos β =
β = 75,52° γ = 180° – 64,05° – 75,52° = 40,43° |
|||||||||||||||||||||||||||||