|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||||||||||||||||
|
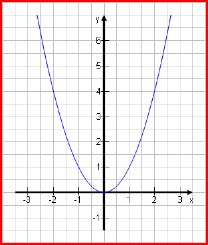
Neben den linearen Funktionen, also den Geraden, spielen in der Mathematik die quadratischen Funktionen eine Hauptrolle. Zeichnet man eine solche Funktion in ein Koordinatensystem, ergibt sich eine Parabel.
Wir erfahren in dieser Lektion, wozu man Parabeln über\\haupt braucht, ihre Wertetabelle zu erstellen und sie zu zeichnen. |
 |
|||||||||||||||||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
| Wozu benötigt man quadratische Funktionen? | ||||||||||||||||||||||||||||||||||||||||||||||
|
Funktionen, etwa y = 2x + 3 oder y = x2 – 4, sind Formeln, mit denen man etwas berechnen kann. In den Naturwissenschaften, in Handwerk und Technik aber auch in der Finanzwelt muss man dauernd etwas berechnen, seien es Preise, benötigte Mengen, Entfernungen oder andere wichtige Daten.
Die einfachste Art von Funktion ist die lineare. Du kennst sie bereits, z.B. y = 2x + 3. Lineare Funktionen kann man anwenden für Probleme, bei denen die Größe, um die es geht, gleichmäßig wächst oder fällt. Mit ihnen berechnest du Handykosten, Einkaufspreise oder Fahrzeiten bei gleichbleibender Geschwindigkeit. |

|
|||||||||||||||||||||||||||||||||||||||||||||
|
Andere Größen verhalten sich nicht linear. So wird ein Wagen, den man beschleunigt, immer schneller. Die pro Sekunde zurückgelegte Strecke wächst dabei quadratisch. Ein Kreis oder eine Kugeloberfläche wird mit zunehmendem Radius ebenfalls quadratisch größer.
"Quadratisch" heißt: Verdoppelt man den Radius, vervierfacht sich die Fläche! Für diese und viele andere Probleme kann man keine linearen Funktionen (Formeln) verwenden. Hier sind quadratische Funktionen angesagt. |
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| Die Funktionsgleichung | ||||||||||||||||||||||||||||||||||||||||||||||
|
Quadratische Funktionen erkennt man daran, dass sie ein x2 als höchste x-Potenz besitzen.
|

|
|||||||||||||||||||||||||||||||||||||||||||||
|
Beispiele:
y = x2 ; y = 3x2 ; y = -x2 ; y = 2x2 + 4x ; y = -3x2 – 6 ; y = x2 + 2x – 4 Keine quadratischen Funktionen wären: y = 4x + 2 (linear) ; y = x3 + 2x2 – 5x (kubisch) |
||||||||||||||||||||||||||||||||||||||||||||||
|
Allgemein haben quadratische Funktionen also folgende Form:
y = ax2 + bx + c Dabei sind a, b und c beliebige Zahlen. Der einfachste Vertreter ist demnach die folgende Funktion: y = x2 Man nennt sie Normalparabel. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
| Wertetabelle und Graph | ||||||||||||||||||||||||||||||||||||||||||||||
|
Um eine Funktion im Koordinatensystem zeichnen zu können, muss man eine Wertetabelle erstellen.
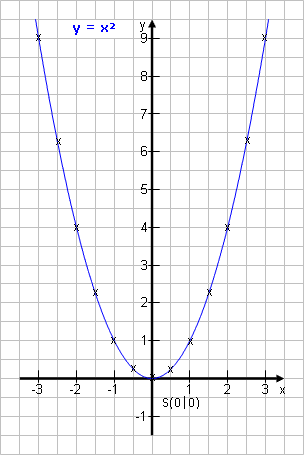
Hierzu berechnet man für unterschiedliche x, was jeweils herauskommt. Beispiel: Erstelle für die Funktion y = x2 eine Wertetabelle für x ϵ [-3 ; 3] und ∆x = 0,5 und zeichne ihren Graph. (also von -3 bis 3, Schrittweite = 0,5) 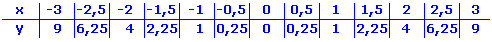 Rechts siehst du das Ergebnis. |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Die Form aller Parabeln ist im Wesentlichen gleich. Sie unterscheiden sich allerdings in ihrer Krümmung. Man kann deshalb nur einige mit der Schablone zeichnen, alle anderen zeichnet man von Hand.
Außerdem unterscheiden sie sich darin, ob sie nach unten oder nach oben geöffnet sind, und darin, wo der Scheitelpunkt liegt. |
||||||||||||||||||||||||||||||||||||||||||||||
|
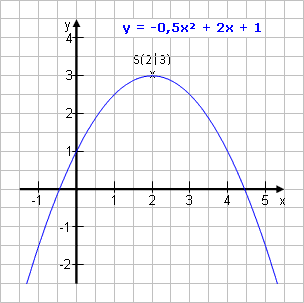
Ein zweites Beispiel
Erstelle für die Funktion y = -0,5x2 + 2x + 1 eine Wertetabelle für x ϵ [-1 ; 5] und ∆x = 1 und zeichne ihren Graph. 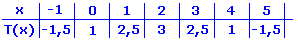 Rechts siehst du wieder das Ergebnis. |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
| Das Problem mit dem Taschenrechner | ||||||||||||||||||||||||||||||||||||||||||||||
|
Beim Eingeben der x-Werte in den Taschenrechner haben viele Schüler arge Probleme, vor allem, wenn es um negative x-Werte geht. Dabei muss man eigentlich nur auf eine Sache achten:
→ Minuszahlen, die quadriert werden, immer in Klammern setzen!!! Versuche es mit der Funktion y = -3x2 – 2x + 1 für x ϵ [-3 ; -1] und ∆x = 1. x = -3: Eingabe: – 3 x ( – 3 ) 2 – 2 x – 3 + 1 → -20 x = -2: Eingabe: – 3 x ( – 2 ) 2 – 2 x – 2 + 1 → -7 x = -1: Eingabe: – 3 x ( – 1 ) 2 – 2 x – 1 + 1 → 0 |
Minuszahlen,
die quadriert werden, immer in Klammern setzen!!! 
|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| Die Bedeutung des Parameters a | ||||||||||||||||||||||||||||||||||||||||||||||
|
Auch ohne Wertetabelle lässt sich eine Parabel grob skizzieren, wenn man versteht, wie sich der Parameter a, also die Zahl vor dem x2, auf die Form auswirkt.
Außer dem Parameter a ist dann noch die Lage des Scheitelpunktes wichtig. Aber den gibt es erst in der nächsten Lektion. |

|
|||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Beispiele:
|
||||||||||||||||||||||||||||||||||||||||||||||