|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Jede Formel (Funktion) kann man vorwärts oder rückwärts benutzen. Vorwärts: Du setzt eine Zahl für x ein und rechnest aus, was raus kommt.
y = x2 + 2x – 1 x=5 → y=? Rückwärts: Du gibst vor, was heraus kommen soll und berechnest, was dazu eingesetzt werden muss. y = x2 + 2x – 1 y=2 → x=? Um das gesuchte x zu bekommen, müssen wir die Gleichung nach x auflösen. Wie das funktioniert, wird gleich gezeigt. Du wirst diese Technik extrem oft brauchen, sowohl bei den Parabeln als auch später in anderen Gebieten wie etwa der Raumgeometrie. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hinführung | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y = 3x2 + 6x – 2 y=7 → x=?
Bei welchem x kommt 7 heraus? Hierzu setzen wir 7 für y ein und versuchen, die Gleichung zu lösen: 7 = 3x2 + 6x – 2 |

|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
So wie bei der Berechnung des Scheitelpunktes gibt es auch hier wieder zwei Wege: Man kann die Sache rechnerisch lösen mit Hilfe der quadratische Ergänzung, oder man greift auf eine Formel zurück.
Diese Formel ergibt sich, wenn man mit den Buchstaben a, b und c statt mit konkreten Zahlen die Sache einmal durchrechnet. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Lösung mit Hilfe der quadratischen Ergänzung | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Wir zeigen hier ein einziges Mal, wie man eine quadratische Gleichung rechnerisch löst. Du kannst später selbst entscheiden, ob du es auf diese Art tust, oder ob du die Formel benutzt.
|
Probe:
Das Ergebnis in die ursprüngliche Gleichung einsetzen und im Kopf nachrechnen, ob die richtige Zahl für y heraus kommt. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
7 = 3x2 + 6x – 2
Das x2 kann letzten Endes nur verschwinden, indem man die Wurzel zieht. Doch dazu muss der Term komplett im Quadrat stehen, nicht nur ein Teil, also (.....)2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ziel erreicht: rechts steht ein Term zum Quadrat. Wir ziehen die Wurzel:
2 = x + 1 ˅ -2 = x + 1 | – 1 Warum das Oder-Zeichen? Weil nicht nur 22 = 4 ist, sondern auch (-2)2! Es gibt also 2 mögliche Lösungen! 1 = x ˅ -3 = x L = {1 ; -3} Wenn du 1 und -3 ganz oben für x einsetzt, wirst du beide Male 7 als Ergebnis heraus bekommen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Die Mitternachtsformel | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Leichter löst sich eine quadratische Gleichung, wenn man die sogenannte Mitternachtsformel anwendet. Aber aufgepasst: Auch hier kann man sich vertun und vertippen, wenn man nicht konzentriert ist!
Zuerst muss man seine Gleichung so umformen, dass auf einer Seite 0 steht. Also z.B. 7 = 3x2 + 6x – 2 | – 7 0 = 3x2 + 6x – 9 allgemein: 0 = ax2 + bx + c |
Außerdem wirst du sie so oft benutzen, dass du um Mitternacht geweckt werden kannst und die Formel auswendig weißt! :O)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dann wird die Gesamtformel in 2 Schritte zerlegt. Man berechnet zunächst den ersten Teil, die Diskriminante:
D = b2 – 4ac hier also: D = 62 – 4·3·(-9) = 144 Nun entscheidet man, ob überhaupt weiter gerechnet wird: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ist die Diskriminante > 0, hat die Gleichung 2 Lösungen.
Ist die Diskriminante = 0, hat die Gleichung 1 Lösung. Ist die Diskriminante < 0, hat die Gleichung keine Lösung. Warum das so ist, werden wir weiter unten sehen. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bei uns ist sie größer als 0 und hat somit zwei Lösungen. Diese erhält man über den zweiten Teil der Formel:
Bei uns:
Die Funktion nimmt also auch hier für x=1 und für x=-3 den Wert 7 an. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ein zweites Beispiel | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Gegeben sei: y = x2 – 3x + 4
Bei welchem x nimmt die Funktion den Wert 2 an? 2 = x2 – 3x + 4 | – 2 0 = x2 – 3x + 2 D = b2 – 4ac = (-3)2 – 4·1·2 = 1 D > 0 → 2 Lösungen
Gar nicht so schwer, oder? :O) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Warum es 0, 1 oder 2 Lösungen geben kann | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sehen wir uns zunächst die Formel an.
Die Gesamtformel hieße eigentlich: x1/2 =
Um den Überblick nicht zu verlieren, berechnen wir zuerst die Diskriminante D = b2 – 4ac. Wie du leicht erkennen kannst, ist das genau der Teil unter der Wurzel. Nun, wenn D>0 ist, müssen wir anschließend die Wurzel aus einer positiven Zahl ziehen, also etwa √4. Dies ergibt immer zwei Lösungen: 2 und -2. |


|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Sollte D hingegen 0 werden, so müssen wir die Wurzel aus 0 ziehen, und die ist 0! √0 = 0
In der Formel fallen dann beide Lösungen zusammen, denn es ist dasselbe, ob man + 0 rechnet oder – 0!
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Wird D sogar negativ, also D<0, dann gibt es überhaupt keine Lösung, denn aus einer Minuszahl kannst du keine Wurzel ziehen. √-4 = nicht definiert! (Es gibt keine Zahl, die zum Quadrat -4 ergäbe.)
In diesem Fall hörst du vorzeitig auf. Du berechnest kein x1 oder x2. Dein Taschenrechner brächte eh nur eine Fehlermeldung. Und du schreibst hin: "Keine Lösung" oder L = {}. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
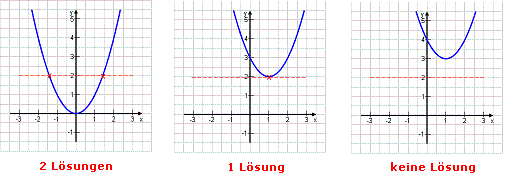
Auch graphisch kann man sehr schön sehen, dass es zwei, eine oder gar keine Lösung geben kann.
Drei Parabeln: y = x2 ; y = x2 – 2x + 3 ; y = x2 – 2x + 4 Wann nehmen die Parabeln den Wert 2 an? Wann ist also y = 2 ? Eine Parabel schneidet die 2, hat also zwei Mal den Wert 2, eine Parabel berührt den Wert nur einmal, und eine liegt schlicht darüber, wird also nie zu 2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| Den Taschenrechner richtig benutzen | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vorsicht beim Eintippen:
0 = 3x2 + 6x – 9 D = 144
Hier musst du darauf achten, dass der Bruchstrich komplett von links nach rechts geht und nicht nur unter der Wurzel verläuft. |

|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Verwende die Bruch-Taste deines Taschenrechners und achte darauf, dass wirklich die richtigen Zahlen oberhalb und die richtigen Zahlen unterhalb des Bruchstrichs landen.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Wenn du mal nur einen alten Taschenrechner zur Verfügung hast, kannst du statt der Bruch-Taste auch "Dividiert" : verwenden. Dann musst du aber sowohl den Zähler als auch den Nenner in Klammern setzen:
( -6 + √144 ) : ( 2 · 3 ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||