|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||
|
Bisher hatten wir, wenn es darum ging, Längen, Flächeninhalte oder Volumina auszurechnen, feste Werte heraus bekommen, einfache Zahlen.
Zahlen bekommt man heraus, wenn es sich um ein einzelnes Problem handelt. Geht es aber um ein allgemeines Problem, ist die Lösung eine Formel. |
 |
||||||||||||||||||||||||
|
Wenn du beispielsweise den Flächeninhalt eines bestimmten Dreiecks berechnest, erhältst du vielleicht das Ergebnis A = 14 cm2. Möchtest du aber allgemein den Flächeninhalt von Dreiecken berechnen, ist das Ergebnis eine Formel. Du kennst sie:
A =
|
|||||||||||||||||||||||||
|
Formeln die man häufig braucht, findet man bereits in der Formelsammlung. Die Formeln, die wir hier erstellen werden, aber nicht, da sie doch recht speziell sind. Wären solche Formeln ebenfalls in der Formelsammlung, würde diese aus allen Nähten platzen.
Es geht auch gar nicht so sehr darum, die Formel irgendwo stehen zu haben, sondern vielmehr darum, zu lernen, wie man selbst auf so eine Formel kommt. |
|||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Hinführung | |||||||||||||||||||||||||
|
Wir beginnen mit Formeln für die Berechnung einer Streckenlänge. Anders ausgedrückt: Mit Formeln für den Abstand zwischen zwei Punkten. Später werden wir auch Formeln für Flächeninhalte erstellen.
Lägen die beiden Punkte, für die wir den Abstand berechnen wollen, an festen Orten, z.B. A(1|2) und B(4|2), so ergäbe sich eine eindeutige Strecke AB . Ihre Länge, also der Abstand zwischen A und B, wäre eine feste Zahl, nämlich 3 (Längeneinheiten).
|
Formeln statt Zahlen
Bei funktionalen Abhängigkeiten geht es immer darum, Formeln aufzustellen. 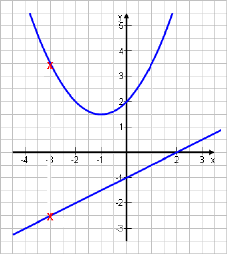 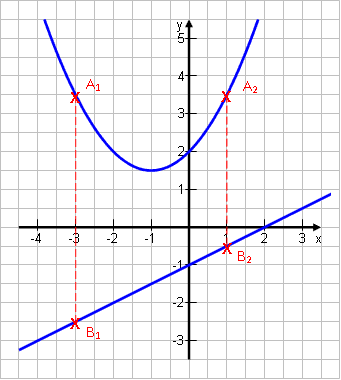
|
||||||||||||||||||||||||
|
Das Besondere ist nun: Unsere Punkte liegen nicht an festen Orten! Unter gewissen Rahmenbedingungen dürfen sie sich "bewegen". Anders ausgedrückt: Die Lage kann unterschiedlich sein. Meistens müssen sie irgendwo auf einer Funktion laufen: auf einer Parabel oder auf einer Geraden.
Nehmen wir als Beispiel die Parabel p und die Gerade g mit p: y = 0,5x2 + x + 2 und g: y = 0,5x – 1 Du siehst beide rechts eingezeichnet. |
|||||||||||||||||||||||||
|
Die Punkte An sollen auf der Parabel liegen, die Punkte Bn genau unten drunter auf der Geraden.
Mathematisch: An ϵ p ; Bn ϵ g Das kleine n deutet an, dass es sich nicht um einen bestimmten Punkt handelt, sondern um viele mögliche: A1, A2, A3 etc. |
|||||||||||||||||||||||||
|
Zeichnen wir zwei Beispiele ein:
Die Punkte A1 und B1 besitzen den x-Wert x = -3. Die Punkte A2 und B2 besitzen den x-Wert x = 1. A1 und B1 liegen übereinander weil sie den gleichen x-Wert besitzen. A2 und B2 ebenfalls. Zum Einzeichnen gehst du einfach auf der x-Achse zur -3 und dann senkrecht hoch bzw. runter auf die beiden Graphen und markierst die Punkte. Genauso für x = 1. |
|||||||||||||||||||||||||
|
Wie man gut sieht, ist der Abstand der Punkte An zu Bn variabel. Der Abstand
A1B1 ist 6 und damit größer als der Abstand A2B2 , der 4 beträgt. Irgendwo zwischen 0 und 1 gibt es wohl den kleinsten Abstand, nach links und nach rechts wird er sehr schnell größer. Der Abstand der Punkte hängt davon ab, bei welchem x-Wert sie liegen. Deshalb brauchen wir für den Abstand eine Formel in Abhängigkeit von x. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Berechnung einer festen Streckenlänge | |||||||||||||||||||||||||
|
Wie berechnet man überhaupt eine Streckenlänge?
Wie man dazu vorgehen muss, überlegen wir uns zunächst an Punkten, die an festen Plätzen liegen. Anschließend wenden wir dieses Wissen an, um die Formel für eine variable Streckenlänge zu finden. |
|
||||||||||||||||||||||||
|
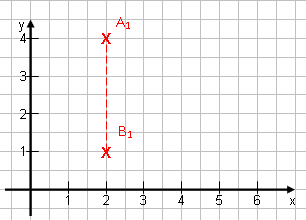
Angenommen, der Punkt A läge auf einer Höhe von y = 4, der Punkt B auf einer Höhe von y = 1. Wie groß ist der Abstand? 3! Klar!
AB = 4 – 1 = 3Methode: Oberer Punkt minus unterer Punkt. Für die Punkte in unserem Beispiel oben bedeutet dies: A1B1 = 3,5 – (-2,5) = 6A2B2 = 3,5 – (-0,5) = 4
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Die Streckenlänge als Formel | |||||||||||||||||||||||||
|
Wenden wir unser Wissen nun an, um die allgemeine Formel in Abhängigkeit vom x-Wert der Punkte zu finden.
Genau wie bei festen Punkten rechnen wir: Oberer Punkt minus unterer Punkt. |


Streckenlänge als Formel
Die Funktionen statt fester Werte einsetzen. |
||||||||||||||||||||||||
|
Aber wie hoch liegt eigentlich der obere Punkt? Da er auf der Parabel liegt, lässt sich seine Höhe, also sein y-Wert über die Parabel-Gleichung ausrechnen.
Und wie hoch liegt der untere Punkt? Da er auf der Geraden liegt, bekommt man seine Höhe, also seinen y-Wert über die Geraden-Gleichung heraus: |
|||||||||||||||||||||||||
|
Oberer Punkt: y = 0,5x2 + x + 2 (auf der Parabel)
Unterer Punkt: y = 0,5x – 1 (auf der Geraden) Abstand = Oben minus Unten: AnBn (x) = 0,5x2 + x + 2 – ( 0,5x – 1)Du musst also nur die Funktionen statt der festen Werte einsetzen. Ausrechnen:
Fertig! |
|||||||||||||||||||||||||
|
Formeln für Situationen, in denen Punkte waagerecht nebeneinander oder schräg voneinander liegen, sind schwieriger zu berechnen. Meistens werden irgendwelche Spezialfälle betrachtet. Diese sollen hier vorerst nicht besprochen werden.
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Ein zweites Beispiel | |||||||||||||||||||||||||
|
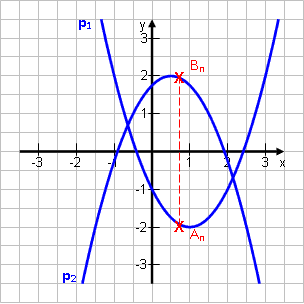
Gegeben seien die Parabeln p1: y = x2 – 2x – 1 und p2: y = -x2 + x + 1,75. An ϵ p1 ; Bn ϵ p2 ; An und Bn haben die gleiche Abszisse x.
Berechne den Abstand AnBn in Abhängigkeit von x im Bereich [-0,64 ; 2,14].
|
|
||||||||||||||||||||||||
|
Wie man sieht, liegt im mittleren Bereich p2 über p1, im äußeren Bereich ist es umgekehrt. Da wir aber die untere von der oberen Funktion abziehen sollen, ist es wichtig, zu wissen, welche oben liegt. Deshalb wurde das Intervall [-0,64; 2,14] angegeben. Wir sollen also im mittleren Bereich rechnen.
Oben minus Unten:
Das wars! |
|||||||||||||||||||||||||