|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||
|
Wir suchen nach weiteren Formeln.
In unserem Einstiegskapitel lagen die beiden Punkte, deren Abstand wir berechneten, immer senkrecht untereinander. Dies ist der einfachste und auch der am häufigsten vorkommende Fall. Welche Koordinaten haben dann eigentlich die beiden Punkte? Und welche Koordinaten hat der zweite Punkt, wenn er nicht mehr senkrecht unter dem ersten liegt, sondern waagerecht oder schräg daneben? |
 |
||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Die Koordinaten des ersten/freien Punktes | |||||||||||||||||||||||||||||
|
Bei funktionalen Abhängigkeiten betrachtet man immer mehrere Punkte, die gemeinsam eine Strecke oder eine Fläche bilden. Dabei beginnt man mit einem freien Punkt, z.B. An, der meist auf einer Parabel oder einer Geraden liegt.
Alle anderen Punkte ergeben sich dann zwangsläufig, weil vorgegeben wird, wie sie in Bezug zu dem ersten Punkt liegen müssen. Zum Beispiel senkrecht unter diesem aber auf einer anderen Geraden, oder waagerecht daneben und um zwei Einheiten weiter rechts, oder um einen bestimmten Vektor im Vergleich zum ersten Punkt verschoben. |


|
||||||||||||||||||||||||||||
|
Der erste Punkt besitzt immer den x-Wert x. Wann immer in der gesamten Aufgabe von x die Rede ist, meint man den x-Wert des ersten Punktes! Meistens heißt der erste, also der frei wählbare Punkt An, aber nicht immer.
An hat dann die Koordinaten: An(x | y) y kann aber noch genauer angegeben werden, denn der Punkt An liegt ja nicht irgendwo im Koordinatensystem, sondern auf dem Graphen einer bestimmten Funktion. |
|||||||||||||||||||||||||||||
|
Liegt der Punkt An beispielsweise auf der Parabel p: y = 2x2 – x + 3, so trägt man deren y-Wert in die Koordinate ein:
An ϵ p: y = 2x2 – x + 3 → An(x | 2x2 – x + 3) Liegt An auf der Geraden g: y = -3x + 4, schreibt man seine Koordinaten folgendermaßen: An ϵ g: y = -3x + 4 → An(x | -3x + 4) Liegt An auf einer Waagerechten mit y = 5: An ϵ g: y = 5 → An(x | 5) |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Bn senkrecht unter/über An | |||||||||||||||||||||||||||||
|
Nun soll es darum gehen, die Koordinaten der anderen Punkte zu berechnen. Starten wir mit dem Fall, der uns bereits bekannt ist.
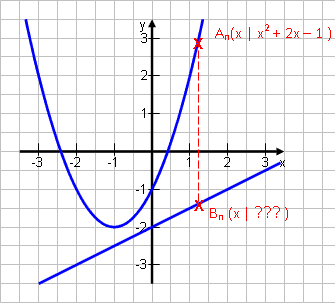
Die Punkte An liegen auf der Parabel p: y = x2 + 2x – 1, die Punkte Bn liegen senkrecht darunter auf der Geraden g: y = 0,5x – 2 An (x | x2 + 2x – 1) Bn ??? Wir müssen uns nun überlegen, welchen x-Wert und welchen y-Wert die Punkte Bn besitzen. |
|
||||||||||||||||||||||||||||
|
x-Wert: Wenn sie senkrecht unter oder über An liegen, bedeutet dies, dass sie den gleichen x-Wert besitzen. Da wir den x-Wert von An aber einfach x nannten, schreiben wir auch für Bn einfach das x. → xB = x
y-Wert: Bn liegt auf der Geraden, also ergibt sich aus x der y-Wert: yB = 0,5x – 2 Ergebnis: Bn (x | 0,5x – 2) |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Bn ergibt sich aus einem Vektor | |||||||||||||||||||||||||||||
|
An liege wieder auf p: y = x2 + 2x – 1:
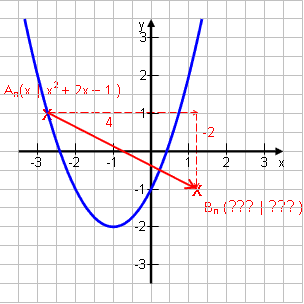
An (x | x2 + 2x – 1) Die Punkte Bn ergeben sich durch eine Verschiebung von An aus um den Vektor
Wir suchen wieder die Koordinaten der Punkte Bn. |
|
||||||||||||||||||||||||||||
|
x-Wert: Durch den Vektor landet der Punkt Bn um 4 weiter rechts als An. → xB = x + 4
y-Wert: Durch den Vektor landet der Punkt Bn um 2 weiter unten als An. → yB = yA – 2 Nun ist der y-Wert von An aber nicht beliebig, sondern x2 + 2x – 1. Deshalb wird der y-Wert von Bn: yB = (x2 + 2x – 1) – 2 = x2 + 2x – 3 Ergebnis: Bn (x + 4 | x2 + 2x – 3) |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Bn verschoben auf der gleichen Funktion | |||||||||||||||||||||||||||||
|
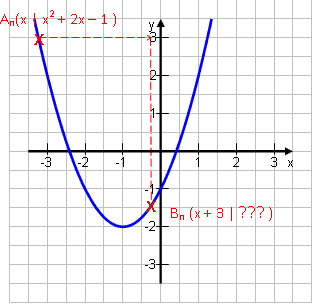
An sei wieder: An (x | x2 + 2x – 1)
Bn sei gegenüber An um 3 nach rechts verschoben und liege ebenfalls auf der Parabel p. |
|
||||||||||||||||||||||||||||
|
x-Wert: Zur Erinnerung: x ist der x-Wert des Punktes An. Bn ist um 3 nach rechts verschoben → xB = x + 3
y-Wert: Bn liegt ebenfalls auf p. Also berechnet man sein y über yB = xB2 + 2xB – 1. Aber Achtung: Der x-Wert des Punktes xB ist nicht einfach x, sonder x + 3. Deshalb setzen wir x + 3 für xB ein: yB = (x + 3)2 + 2(x + 3) – 1 = x2 + 6x + 9 + 2x + 6 – 1 = x2 + 8x + 14 Ergebnis: Bn (x + 3 | x2 + 8x + 14) |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Bn verschoben auf einer anderen Funktion | |||||||||||||||||||||||||||||
|
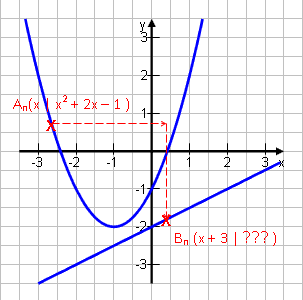
An sei wieder: An (x | x2 + 2x – 1)
Bn sei gegenüber An um 3 nach rechts verschoben und liege auf der Geraden g: y = 0,5x – 2. |
|
||||||||||||||||||||||||||||
|
x-Wert: xB = x + 3
y-Wert: Bn liegt auf der Geraden. Also berechnet man sein y über yB = 0,5xB – 2. Für xB setzen wir x + 3 ein: yB = 0,5·(x + 3) – 2 = 0,5x + 1,5 – 2 = 0,5x – 0,5 Ergebnis: Bn (x + 3 | 0,5x – 0,5) |
|||||||||||||||||||||||||||||
|
Läge der Punkt Bn nicht auf einer anderen Geraden sondern auf einer anderen Parabel, zB. p2: y = -x2 + 3x – 1, so hätten wir das verschobene xB, also x + 3, in diese Parabelgleichung einsetzen müssen:
yB = -(x + 3)2 + 3·(x + 3) – 1 = -(x2 + 6x + 9) + 3x + 9 – 1 = -x2 – 3x – 1 Ergebnis: Bn (x + 3 | -x2 – 3x – 1) |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Bn waagerecht neben An auf der gleichen Funktion | |||||||||||||||||||||||||||||
|
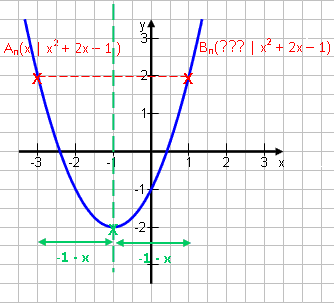
An sei wieder: An (x | x2 + 2x – 1)
Bn soll nun waagerecht daneben auf dem anderen Ast der Parabel liegen. y-Wert: Der gleiche wie bei An: → yB = x2 + 2x – 1 x-Wert: Der x-Wert ergibt sich dadurch, dass Bn genauso weit von der Symmetrie-Achse, also vom Scheitelpunkt, entfernt ist wie der Punkt An, nur eben rechts davon liegt statt links. |
Schwierig!
|
||||||||||||||||||||||||||||
|
Der Scheitelpunkt ist S(-1|-2). Wie weit ist An vom Scheitelpunkt entfernt? Der x-Wert -3 ist z.B. genau 2 von S entfernt. Der x-Wert -5 ist genau 4 davon entfernt.
Da man den waagerechten Abstand zweier Punkte dadurch erhält, dass man den rechten x-Wert (hier -1) minus den linken x-Wert (hier x) berechnet, ergibt sich für den waagerechten Abstand eines Punktes zum Scheitelpunkt: Abstand = -1 – x Der x-Wert des Punktes Bn ist genauso weit vom Scheitelpunkt entfernt, also ebenfalls -1 + x. Und wo liegt er? Genau in dieser Entfernung rechts vom Scheitelpunkt, also: xB = -1 + (-1 – x) = -x – 2 Ergebnis: Bn (-x – 2 | x2 + 2x – 1) |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Bn waagerecht neben An und auf anderer Funktion | |||||||||||||||||||||||||||||
|
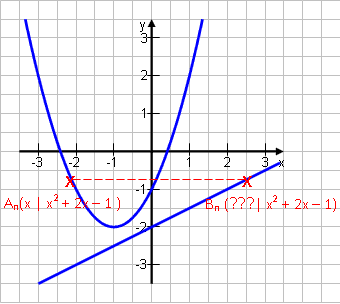
An sei wieder: An (x | x2 + 2x – 1)
Bn liege immer auf gleicher Höhe waagerecht daneben, aber auf der Geraden y = 0,5x – 2. y-Wert: gleiche Höhe, also berechnet sich der y-Wert von Bn einfach aus dem y-Wert von An: → yB = x2 + 2x – 1!! |
Schwierig!
|
||||||||||||||||||||||||||||
|
x-Wert: Der x-Wert ergibt sich, wenn man fordert, dass bei der Geraden der gleiche y-Wert heraus kommt wie bei der Parabel:
Ergebnis: Bn (2x2 + 4x + 2 | x2 + 2x – 1) |
|||||||||||||||||||||||||||||
|
Entwarnung: Kommt sehr selten vor. :O)
|
|||||||||||||||||||||||||||||