|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Wir übertragen unser Wissen aus der Dreiecksberechnung auf dreidimensionale Körper. In den Körpern berechnen wir unbekannte Strecken und Winkel, ihre Oberfläche und ihr Volumen. Außerdem lernen wir, wie man Körper im Schrägbild darstellt.
Begonnen wird mit Prismen, den am regelmäßigsten aufgebauten und damit einfachsten Körpern. |
 |
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Woran man Prismen erkennt. | |||||||||||||||||||||||||||||||
|
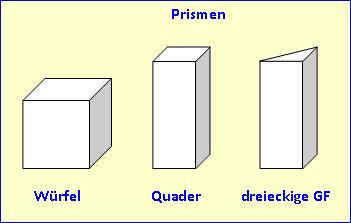
Prismen sind alle eckigen Körper, die oben genauso aussehen sind wie unten, also nicht spitz zusammen oder auseinander laufen.
Gerade Prismen laufen dabei senkrecht nach oben, schiefe Prismen in einem bestimmten Winkel. Wir beschäftigen uns in der Regel nur mit geraden Prismen. |
|
||||||||||||||||||||||||||||||
|
Die bekanntesten Vertreter sind der Würfel und der Quader. Wenn du eine Toblerone-Schachtel aufrecht hinstellst, hast du ein Beispiel für ein Prisma mit dreieckiger Grundfläche. Viele Schüler besitzen eine Riesenpackung von Stabilo-Stiften – ein Prisma mit sechseckiger Grundfläche.
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Schrägbilder zeichnen | |||||||||||||||||||||||||||||||
|
Schrägbilder zeichnet man folgendermaßen:
Zunächst wird die Schrägbildachse gezeichnet. Alle Linien parallel zur Zeichenebene zeichnet man in Originalgröße. Also ganz einfach. Aufpassen muss man aber auf alle Linien, die senkrecht zur Zeicheneben verlaufen. Das sind die Linien, die dem Körper seine 3D-Eigenschaft geben. Die das Blatt also quasi durchstoßen wollen. Diese Linien werden unter einem Winkel ω zur Waagerechten gezeichnet. ω ist meistens 45°. Also zeichnet man um 45° schräg nach oben. Außerdem verkürzt man sie um den Faktor q. q ist meistens 0,5. Somit verkürzt man die Linien um die Hälfte. Linien, die irgendwie schräg zur Zeichenebene verlaufen, wie Diagonalen oder irgendwelche schrägen Linien im Körper, darf man nicht abmessen! Sie müssen dadurch erzeugt werden, dass man zwei vorhandene Punkte verbindet. |
Achtung!
Schräg (meist 45°) nach hinten laufende Linien um den Faktor q (meist um die Hälfte) verkürzen! 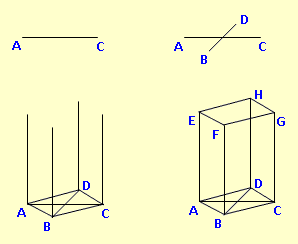
|
||||||||||||||||||||||||||||||
|
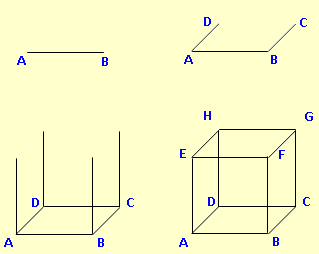
Beispiel 1:
Zeichne das Schrägbild eines Würfels mit der Grundseite ABCD und einer Kantenlänge von 5 cm. AB soll die Schrägbildachse sein. ω = 45° , q = 0,5. Zunächst zeichnest du die untere, vordere Kante [AB]. Dann [BC] und [AD] unter 45° schräg nach oben. Allerdings nur 2,5 cm lang, weil ja um den Faktor 0,5 verkürzt wird. Damit wird die Zeichnung dreidimensional. Zum Schluss die vier Außenkanten senkrecht nach oben. Oben alles verbinden. Fertig. Die Linien, die eigentlich durch vordere Teile des Körpers verdeckt wären, kannst du gestrichelt zeichnen. Hilft später beim Rechnen, muss aber nicht unbedingt sein. |
|||||||||||||||||||||||||||||||
|
Beispiel 2:
Zeichne das Schrägbild eines Quaders mit der quadratischen Fläche ABCD als Grundseite und der Höhe [AE]. AB = 6 cm. Höhe AE = 10 cm. Die Diagonal [AC] soll die Schrägbildachse sein. ω = 45° , q = 0,5.Schon schwieriger! Wir müssen mit der Diagonalen beginnen. Aber wie lang ist diese? Sie muss zunächst über Pythagoras berechnet werden: AB = √6² + 6² = 8,49 cmNun würden wir gerne an beiden Enden die vier unteren Kanten einzeichnen. Geht aber nicht! Denn diese Kanten laufen in Wirklichkeit nicht senkrecht nach hinten sondern in einem 45°-Winkel, weil der Körper ja gedreht ist. Und 45° im Original sind bei uns noch lange keine 45°!!! Die einzige Linie, die senkrecht nach hinten läuft, ist die zweite Diagonale. Also zeichnen wir diese in der Mitte der ersten Diagonalen ein. 45° schräg nach oben! Um die Hälfte verkürzt, also 4,25 cm lang. Davon wiederum die Hälfte nach hinten und die Hälfte nach vorn. Nun die Seitenkanten dran, oben alles verbinden. Fertig. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Volumen und Oberfläche | |||||||||||||||||||||||||||||||
|
Eine der häufigsten Fragen, die man sich bei einem Prisma stellt, ist die, welches Volumen es hat:
Volumen = Grundfläche mal Höhe. Bei der Grundfläche kommt es darauf an, um welche Figur es sich handelt:
Die Oberfläche ist die komplette von außen erreichbare Fläche, also auch die Unterseite. Da man die Grundfläche oben ja noch einmal hat, quasi als Deckel, ergibt sich: Oberfläche = 2·Grundfläche + Mantelfläche Die Mantelfläche ist die Fläche außen rum. Bei einem Würfel sind das vier Quadrate. Bei einem Quader vier Rechtecke, von denen je zwei gleich sind. Bei einem Toblerone-Prisma sind es drei gleiche Rechtecke usw. |

Man merkt sich
nur die Methode, nicht die einzelnen Formeln.  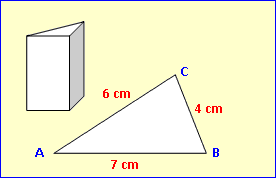 |
||||||||||||||||||||||||||||||
|
Beispiel 1:
Gegeben ist ein Quader mit der Grundfläche ABCD. AB = 4 cm ; BC = 6 cm ; Höhe AE = 3 cm.Berechne Volumen und Oberfläche des Körpers. V = 4 · 6 · 3 = 72 cm3 O = 2·4·6 + 2·4·3 + 2·6·3 = 108 cm2 |
|||||||||||||||||||||||||||||||
|
Beispiel 2:
Gegeben ist ein Prisma mit der der dreieckigen Grundfläche ABC. AB = 7 cm ; BC = 4 cm ; AC = 6 cm. Die Höhe AD des Prismas beträgt 5 cm.Berechne Volumen und Oberfläche des Körpers. Für die Grundfläche brauchen wir die Dreiecks-Höhe oder einen Winkel. Kosinussatz: 42 = 62 + 72 – 2·6·7·cos α α = 34,77° G = 0,5 · 6 · 7 · sin 34,77° = 11,98 cm2 V = G · h = 11,98 · 5 = 59,9 cm3 O = 2·G + M = 2·11,98 + 7·5 + 4·5 + 6·5 = 108,96 cm2 |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Berechnungen im Prisma | |||||||||||||||||||||||||||||||
|
Im Prisma ist man oft an Seitendiagonalen und Raumdiagonalen interessiert, sowie den Winkeln, die diese mit einer Kante oder einer Fläche einschließen.
Da alle Kanten und Seiten im geraden Prisma rechte Winkel bilden, arbeitet man vor allem mit Pythagoras, Sinus, Kosinus und Tangens. |
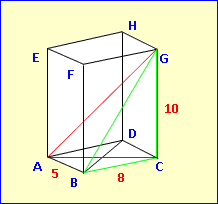 
∡CBG:
Du gehst von C über B nach G. Der Winkel liegt also immer beim mittleren Punkt! |
||||||||||||||||||||||||||||||
|
Beispiel 1:
Im nebenstehenden Prisma sind AB = 5 cm, BC = 8 cm und AE = 10 cm.Berechne die Längen der Flächendiagonalen [BG] sowie der Raumdiagonalen [AG]. Die Flächendiagonalen erledigt man einfach mit Pythagoras in ihrer Fläche. BG 2 = 82 + 102 | √ BG = 12,81 cmFür die Raumdiagonale verwenden wir das Dreieck ACG. Hier berechnen wir zunächst die Diagonale [AC] am Boden. Das Dreieck ABC am Boden ist rechtwinklig. Deshalb geht Pythagoras. AC 2 = 52 + 82 | √ AC = 9,43 cmAuch das Dreieck ACG ist bei C rechtwinklig. Deshalb also noch einmal die gleiche Technik. AG 2 = 9,432 + 102 | √ AG = 13,74 cm
|
|||||||||||||||||||||||||||||||
|
Beispiel 2:
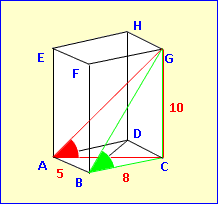
Berechne im gleichen Prisma den Winkel ∡CBG, den Die Flächendiagonale [BG] mit der Grundfläche einschließt, sowie den Winkel ∡CAG, den die Raumdiagonale mit der Grundfläche einschließt. Wieder suchen wir uns Dreiecke, in denen die gesuchten Winkel berechnet werden können. Und – oh Wunder – sie sind wieder rechtwinklig. tan ∡CBG =
∡CBG = 51,34° tan ∡CAG =
∡CBG = 46,68° |
|||||||||||||||||||||||||||||||