|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nicht mehr ganz so einfach wie der Zylinder ist der Kegel. Eine kreisrunde Grundfläche, die nach oben hin zu einer Spitze zusammen läuft. Eine Art runde Pyramide also. Wegen der schrägen Außenkante lässt sich allerdings etwas mehr berechnen als beim Zylinder.
Der absolute Langweiler ist die Kugel. Nur einfachste Rechnungen! Eis in der Tüte vereint übrigens beides: einen Kegel (umgedreht) und ein paar Kugeln. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Kegel und Kugel im Axialschnitt | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
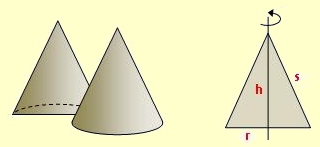
Kegel sind Körper mit runder Grundfläche,
die zu einer Spitze hin zusammen laufen. Schneiden wir den Kegel in der Mitte durch, ergibt sich eine gleichschenklige Dreiecksfläche. Anders ausgedrückt: Lässt man ein gleichschenkliges Dreieck um seine Symmetrie-Achse rotieren, ergibt sich ein Kegel. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
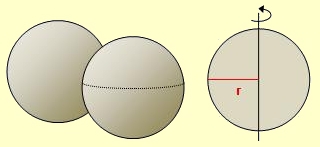
Kugeln sind Körper, die ...
... kugelrund sind. ;-) Die Kugel wird im Axialschnitt zu einer Scheibe. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Formeln für den Kegel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Volumen:
Das Volumen des Kegels ist ein Drittel von dem des entsprechenden Zylinders. Das ist wie bei Pyramide-Prisma. Läuft der Körper oben spitzt zu, bleibt nur noch ein Drittel des Volumens. V =
Oberfläche: Die Oberfläche besteht aus Grundfläche und Mantel. Der Mantel berechnet sich über:
Damit ergibt sich für die Oberfläche: O = G + M = π·r2 + π·r·s Mantellinie und Winkel: s, r und h stehen über Pythagoras in Beziehung: s2 = r2 + h2 Für den Winkel α in der Spitze des Kegels gilt: tan (
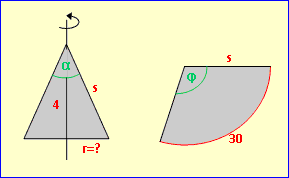
Rollt man den Mantel aus, erhält man einen Kreissektor, dessen Bogenlänge der ursprüngliche Umfang des Kegels ist. In diesem Kreissegment findet man einen neuen Mittelpunktswinkel φ, der nicht identisch ist mit dem Winkel in der Spitze des Kegels.
|


|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Beispiel:
Ein Kegel besitze einen Umfang von 30 cm und eine Höhe von 4 cm. Berechne Volumen und Oberfläche, den Öffnungswinkel α in der Kegelspitze sowie den Mittelpunktswinkel φ der aufgerollten Mantelfläche. Lsg: Zunächst benötigen wir den Radius. Wir erhalten ihn über den Umfang: 30 = 2·π·r | : 2 : π r = 4,77 cm V =
s = √4,77² + 4² = 6,23 cm O = π·4,772 + π·4,77·6,23 = 164,84 cm2 tan (
α = 100,04°
φ = 275,63° |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Formeln für die Kugel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Volumen: V =
Oberfläche: O = 4 · π · r2 |

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Beispiel: Berechne Volumen und Oberfläche einer Eiskugel mit dem Durchmesser 7 cm (Megakugel, Zitrone). V =
O = 4 · π · 3,52 = 153,94 cm2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||